Методы моделирования ионосферы

Модель измерений

Cпутниковая навигация основывается на использовании принципа беззапросных дальномерных измерений между навигационными спутниками и потребителем. Измеренная дальность отличается от истинной на величину различных задержек и ухода часов, поэтому называется псевдодальностью. Представленная модель открытых навигационных измерений отличается от общепринятой тем, что в ней систематические кодовые ошибки разделены отдельно на ошибки приемника и спутника, при этом систематические ошибки для каждого приемника в общем случае различны для каждого спутника. Это особенно актуально для системы ГЛОНАСС, поскольку позволяет учитывать особенности частотного разделения сигналов и более точно калибровать приемники системы ГЛОНАСС.

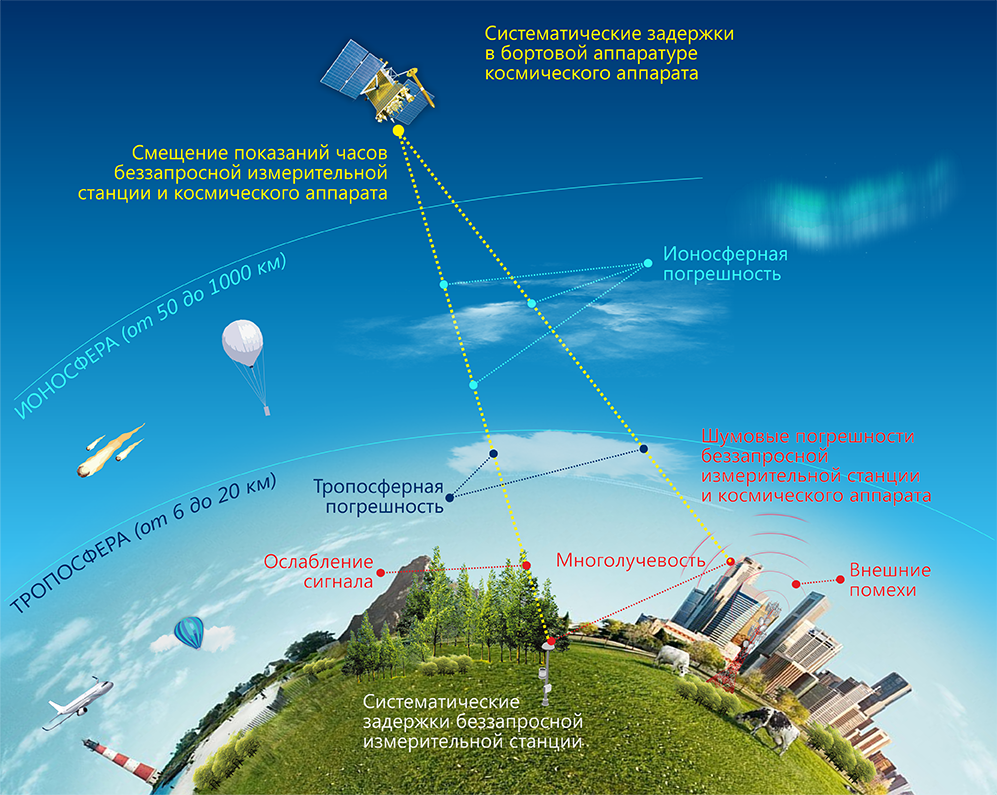
Рис. 1. Составляющие измерений псевдодальности ГНСС

Математическая модель измерений псевдодальностей открытых навигационных сигналов ГНСС стандартной точности (СТ) поддиапазонов L1 и L2 (С1С и C2C в обозначениях RINEX-3 [1]) может быть представлена в следующем виде:

\[ P_{GS,C1}^{SC} = \overline{P_{GS}^{SC}} + I_{GS,1}^{SC} + b_{GS(SC),C1} + b_{C1}^{SC} + \varepsilon_{GS,C1}^{SC} \]

\[ P_{GS,C2}^{SC} = \overline{P_{GS}^{SC}} + I_{GS,2}^{SC} + b_{GS(SC),C2} + b_{C2}^{SC} + \varepsilon_{GS,C2}^{SC} \]

где,

\(\overline{P_{GS}^{SC}} = \overline{\rho_{GS}^{SC}} + T_{GS}^{SC} + c(dt_{GS} - dt^{SC}) \) - расчетные значения псевдодальностей с учетом тропосферной погрешности \(T_{GS}^{SC}\) и смещений показаний часов беззапросной измерительной станции и космического аппарата \(c(dt_{GS} - dt^{SC})\);

\(\overline{\rho_{GS}^{SC}}\) — истинная дальность;

\(b_{GS(SC),C1} , b_{GS(SC),C2}\) — систематические задержки БИС для C1, C2, в общем случае зависят и от КА;

\(b_{C1}^{SC} , b_{C2}^{SC}\) — систематические задержки в бортовой аппаратуре КА для C1, C2;

\(\varepsilon_{GS,C1}^{SC} , \varepsilon_{GS,C2}^{SC}\) — шумовые погрешности кодовых измерений С1С, C2С псевдодальности КА и БИС.

Под картами ионосферы в данном описании подразумеваются карты полного электронного содержания TEC (Total Electron Content) в ионосфере, поскольку только свободные электроны в ионосфере влияют на задержку радиосигнала.

Ионосферная задержка зависит от частоты и электронного содержания вдоль всего пути сигнала (англ. STEC — Slant Total Electron Content):

\[ I = \frac{40.31 m^3 s^{-2}}{f^2} \cdot \int N_e d l = \frac{40.31 m^3 s^{-2}}{f^2} \cdot STEC \]

Для вычисления параметров ионосферы и ДКЗ (англ. DCB — Differential Code Bias) используется так называемая безгеометрическая комбинация кодовых измерений на двух частотах:

\[ P_{GS,C1-C2}^{SC,GF} = P_{GS,C1}^{SC} - P_{GS,C2}^{SC} = 40.31(\frac{1}{f_1^2} - \frac{1}{f_2^2}) \cdot STEC + DCB_{GS,C1-C2}^{SC} + \varepsilon_{GS,C1-C2}^{SC,GF} \]

Общая межчастотная дифференциальная кодовая задержка равна сумме задержек КА и БИС и определяется следующим образом:

\[ DCB_{GS,C1-C2}^{SC} = DCB_{GS(SC),C1-C2} + DCB_{C1-C2}^{SC} = ( b_{GS(SC),C1} - b_{GS(SC),C2} ) + ( b_{C1}^{SC} - b_{C2}^{SC} ) \]

Однослойная модель ионосферы

в случае однослойной модели ионосфера рассматривается как тонкая оболочка постоянной высоты \(h\). Наклонное электронное содержание \(STEC\) определяется умножением вертикального полного электронного содержания \(VTEC\) (Vertical Total Electron Content) на функцию отображения \(m(E)\), которая зависит от угла места \(E\), высоты слоя ионосферы \(h\) = 450 км и радиуса Земли \(R_\bigoplus\) :

\[ STEC = VTEC \cdot m(E) = VTEC \cdot \frac{1}{sin(E')} \]

\[ cos(E') = \frac{R_\bigoplus}{R_\bigoplus + h} \cdot cos(E) \]

где \(E’\) — угол места в точке прокола ионосферы.

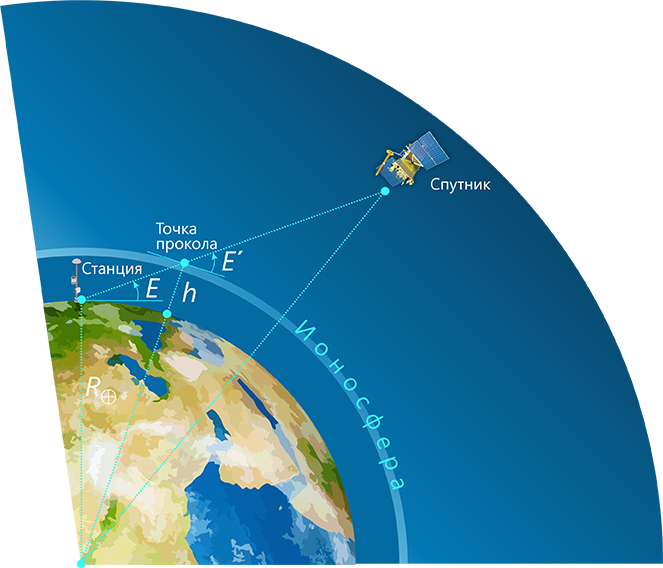
Рис. 2. Однослойная модель ионосферы

В терминологии международной службы анализа IGS межчастотные задержки называются дифференциальными кодовыми задержками (\(DCB\)), в ИКД зарубежных систем - GD (Group Delay), в ИКД ГЛОНАСС — смещения излучаемых навигационных радиосигналов поддиапазона L2 относительно навигационных радиосигналов поддиапазона L1. Поскольку ионосферная погрешность измерений обратно пропорциональна квадрату частоты, для определения задержек \(DCB\) требуется знание ионосферы.

Предполагается, что разность измерений в поддиапазонах L1 и L2 обусловлена только ионосферой, задержками DCB, шумовыми погрешностями измерений и многолучевостью. Суммарный вклад шумовых погрешностей и многолучевости современной НАП геодезического класса как правило не превосходит 1 м даже на относительно низких углах места 10…20°, т.е. эти ошибки многократно снижаются при большом числе измерений.

Строгое разделение наблюдаемой каждой станцией суммарной дифференциальной кодовой задержки на составляющие за счет КА и станций невозможно. Для разделения используется предположение о равенстве нулю суммы всех бортовых межчастотных задержек, а также использование некоторого эталона, в качестве которого может выступать «средний приемник по сети», либо несколько выбранных откалиброванных приемников [4].

Расчет дифференциальных кодовых задержек проводится в два этапа:

• На первом этапе рассчитывается суммарная дифференциальная задержка КА-БИС \(DCB_{GS,C1-C2}^{SC}\) по сети глобально распределенных приемников;
• На втором этапе происходит разделение суммарной задержки и вычисляются дифференциальные кодовые задержки отдельно для КА \(DCB_{C1-C2}^{SC}\) и станции \(DCB_{GS.C1-C2}\)

Далее рассмотрены три различных способа [5] моделирования полного электронного содержания TEC в ионосфере и уточнения суммарных задержек DCB:

1. уточнение дифференциальных кодовых задержек DCB с помощью существующих карт ионосферы;
2. моделирование локальной ионосферы и уточнение дифференциальных кодовых задержек DCB;
3. построение глобальных карт ионосферы и уточнение дифференциальных кодовых задержек DCB.

Уточнение дифференциальных кодовых задержек DCB с помощью существующих карт ионосферы

Первый способ уточнения суммарных дифференциальных кодовых задержек \(DCB_{GS,C1-C2}^{SC}\) относительно прост и применяется, когда ионосферная задержка заранее известна [6].

Например, можно использовать существующие глобальные ионосферные карты TEC, которые публикуются в открытом доступе в формате IONEX [2] зарубежными центрами анализа IGS [13, 14]. Также с 2021 года общедоступны ежесуточные глобальные ионосферные карты TEC по расчетам ИАЦ КВНО [11].

Для определения суммарной дифференциальной кодовой задержки достаточно измерений одной станции по одному КА на суточном интервале, задержка \(DCB_{GS,C1-C2}^{SC}\) уточняется как среднее арифметическое всех безгеометрических комбинации измерений:

\[ DCB_{GS,C1-C2}^{SC} = \frac{1}{n} \displaystyle\sum_{i=1}^{n} (P_{GS,C1-C2}^{SC,GF} - I_{GS}^{SC,GF}) \]

где эквивалентная ионосферная задержка для безгеометрической комбинации задержки определяется по ранее описанному принципу:

\[ I_{GS}^{SC,GF} = 40.31 m^3 s^{-2} \cdot (\frac{1}{(f_1^{SC})^2} - \frac{1}{(f_2^{SC})^2}) \cdot m(E) \cdot VTEC \]

Для примера на рис.3 отображено положение станции, красным цветом отмечена подспутниковая трасса одного КА в двух зонах видимости этой станции на суточном интервале, синим цветом обозначены соответствующие точки прокола ионосферы:

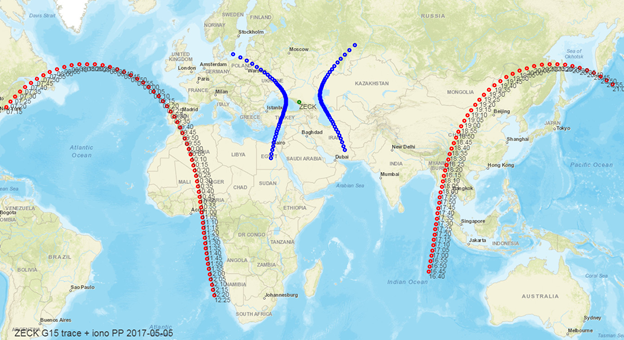
Рис.3. Трассы КА ГЛОНАСС и соответствующие точки прокола для одной станции

На рис.4 представлен процесс расчета. Из безгеометрической комбинации измерений (красный цвет) вычитается известная ионосферная задержка (синий цвет), полученная разность усредняется (зеленый цвет). Таким образом вычисляется искомая дифференциальная кодовая задержка.

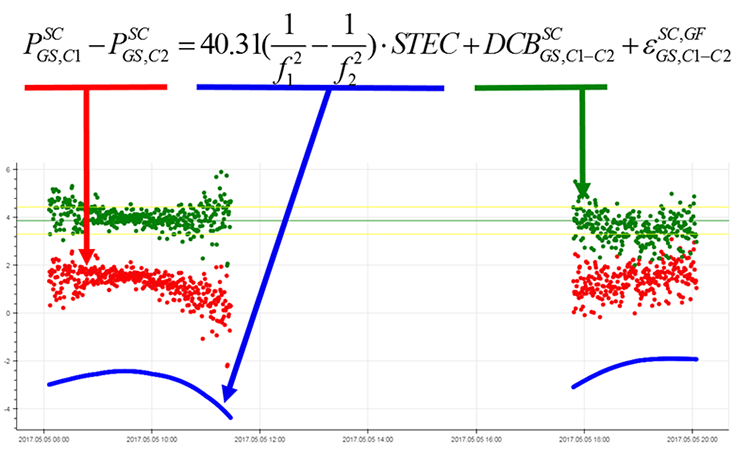
Рис.4. Безгеометрическая комбинация (красный), ионосферная задержка (синий), суммарная дифференциальная кодовая задержка (зеленый)

Моделирование локальной ионосферы и уточнение дифференциальных кодовых задержек DCB

Второй метод определения суммарных дифференциальных кодовых задержек заключается в одновременном уточнении дифференциальных кодовых задержек \(DCB_{GS,C1-C2}^{SC}\) и параметров локальной ионосферы. Уточнение выполняется для одной станции и всех наблюдаемых КА методом наименьших квадратов (МНК). Преимуществом данного метода является его автономность и лучшая точность. Метод моделирования локальной ионосферы в виде двумерного полинома был представлен в 1999 году [7]. Позднее этот метод был усовершенствован: к полиному добавилось дополнительное слагаемое в виде разложения в конечный ряд Фурье [8, 9].

Таким образом, полное электронное содержание в локальной области станции моделируется в зависимости от географической широты \(\varphi\) и солнечно-фиксированной долготы \(t\) в точке прокола:

\[ VTEC(\varphi,t) = \displaystyle\sum_{n=0}^{n_{max}} \displaystyle\sum_{m=0}^{m_{max}} \{ E_{nm} (\varphi - \varphi_0)^n \cdot t^m \} + \displaystyle\sum_{k=0}^{k_{max}} \{ C_k cos(k \cdot t) + S_k sin(k \cdot t) \} \]

где \(\varphi\) – географическая широта точки прокола ионосферы;

\(\varphi_0\) – географическая широта станции;

\( t = \lambda — \lambda_{SUN} \) - географическая долгота точки прокола ионосферы, скорректированная на положение Солнца, в единицах времени обозначается как местное солнечное время;

\(E_{nm}\) – неизвестные коэффициенты полинома;

\(C_k\) и \(S_k\) – неизвестные коэффициенты разложения в ряд Фурье.

Ненаблюдаемость задачи исключается подбором степени полинома \( ( m_{max}, n_{max}=4 ) \), количества коэффициентов ряда Фурье \( (k_{max}=4 ) \), а также уточнением параметров для одной станции и всех КА (всех ГНСС), по которым есть измерения. Точки прокола ионосферы и примерная область уточнения параметров ионосферы на суточном интервале представлена на рис.5.

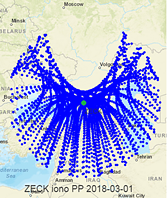
Рис.5. Точки прокола ионосферы для одной станции на суточном интервале

После расчета параметров локальной модели ионосферы и суммарных дифференциальных задержек DCB можно разделить систематики на сумму дифференциальных кодовых задержек КА и БИС [8, 9]. Для решения данной задачи необходим некоторый эталон, в качестве которого могут использоваться калиброванные приемники, либо «средний приемник» по сети. Полученные итоговые DCB хранятся в файлах формата SINEX_BIAS [3], которые публикуются центрами международной службы анализа IGS [15].

В ИАЦ КВНО расчет параметров локальной ионосферы и разделение дифференциальных задержек проводится с 2017 года, итоговые задержки DCB в формате SINEX_BIAS публикуются на ежедневной основе [12]. Реализован расчет дифференциальных кодовых задержек с учетом литерной зависимости ГЛОНАСС как с помощью «среднего приемника» по сети, так и с помощью калиброванного приемника [4].

Построение глобальных карт ионосферы и уточнение дифференциальных кодовых задержек DCB

Построение глобальных ионосферных карт TEC (англ. GIM – Global Ionosphere Map) схоже с построением локальных карт ионосферы по измерениям одной станции, но для вычисления используется уже глобально распределенная сеть станций.

С помощью МНК на ежесуточной основе уточняются одновременно все дифференциальные кодовые задержки DCB для всех пар КА-БИС и распределение вертикального полного электронного содержания \(VTEC\) в ионосфере в виде разложения по сферическим гармоникам в зависимости от широты и солнечно-фиксированной долготы:

\[ VTEC(\varphi,t) = \displaystyle\sum_{n=0}^{n_{max}} \displaystyle\sum_{m=0}^{n} P_{nm} sin \varphi \{ C_{nm} cos (mt) + S_{nm} sin(mt) \} \]

где \(\varphi\) – широта точки прокола ионосферы;

\( t = \lambda — \lambda_{SUN} \) - долгота точки прокола ионосферы, скорректированная на положение Солнца;

\(P_{nm}\) – полиномы Лежандра;

\(С_{nm}\) и \(S_{nm}\) – неизвестные коэффициенты сферических функций.

В модели могут использоваться как географические, так и геомагнитные координаты.

Метод расчета глобальных карт ионосферы опубликован в 1999 году [7]. В первое время уточнялся один набор дифференциальных кодовых задержек DCB и один набор коэффициентов сферических функций для суточного интервала. Затем метод был усовершенствован [10], стали уточнятся 25 или 13 наборов коэффициентов по сферическим функциям для 1-часового или 2-часового шага расчета. Между последовательными коэффициентами может добавляться условие связи, например, кусочно-линейная зависимость:

\[ X(t) = (1 - \Delta_i(t))X(T_i) + \Delta_i(t) X(T_{i+1}), i = 1 \dots 25 \]

где \(X(t)\) – коэффициент разложения по сферическим функциям в момент времени \(t\);

\(X(T_i)\) и \(X(T_{i+1})\) – уточняемые коэффициенты разложения;

\( \Delta_i(t) = \frac{t - T_i}{T_{i+1} - T_i}\) - вес момента времени \(t\) между \(T_i\) и \(T_{i+1}\).

При построении глобальных карт ионосферы существует сложность уточнения параметров в географических зонах, где отсутствуют измерения ГНСС, в частности, над океанами. Так как аргументами являются широта и солнечно-фиксированная долгота, то в качестве решения данной проблемы используется экстраполяция по времени с низким весом фактических измерений на пустые пространственные зоны. Другими словами, используется предположение, что в конкретной географической точке параметры ионосферы соответствуют параметрам ионосферы восточнее на 15°, но 1 ч назад.

Глобальные карты ионосферы хранятся в формате IONEX [2]. Файлы IONEX по расчетам различных центров анализа IGS общедоступны [13, 14].

В ИАЦ КВНО расчет выполняется по открытым измерениям около 300 станций сети международной службы IGS, используются измерения систем ГЛОНАСС и GPS. Результаты публикуются в формате IONEX c 2021 года на ежедневной основе [11]. Пространственное разрешение 2,5° по широте, 5° по долготе, шаг по времени 2 ч.

СПИСОК ИСТОЧНИКОВ

• Система контроля и подтверждения характеристик ГНСС
• FTP-архив
• Нормативно-правовые документы в области спутниковой навигации
• Пилотные проекты